Well, but every purely attractive potential has a bound state in 1D also the delta potential. Physics Forums - The Fusion of Science and Community. One‐Dimensional Quantum Mechanics. Finite Potential well: Finite number of bound states, energy spacing smaller since wave function more spread out.

@user120404 Yes, the state is a superposition of the stationary states of the well (width $2L$), with coefficients $c_n$ determined from the initial wave function equal to the ground state of a well of width $L$. The way I've chosen to approach this problem, the well has width $2L$ at $t=0$, so there is no expansion of the well.

Finally, I'm not sure what you mean when you say 'assuming the new wavefunction is the ground state of the new well.' Do you mean 'assuming a measurement of the energy yields the ground-state energy of the well of width $2L$?' – Jan 8 at 16:03 •. It seems like the thing you are missing is a very basic ingredient of quantum mechanics -- the Born rule. When we make a measurement of some observable $A$, we will find that $A$ takes values in the eigenvalues $a_i$ of the corresponding operator $A$.

The Born rule tells us that, for a system initially in the state $ left psi right>$, the probability of finding the system in the eigenstate $ left a_i right>$ corresponding to eigenvalue $a_i$ is $ left left right ^2$. In standard mathematics notation, this is $ left (a_i, psi) right ^2$, the inner product between the the two states. In the position basis, the states are wavefunctions, and we can write their inner product explicitly as $ int,dx, phi_i(x) psi(x)$.

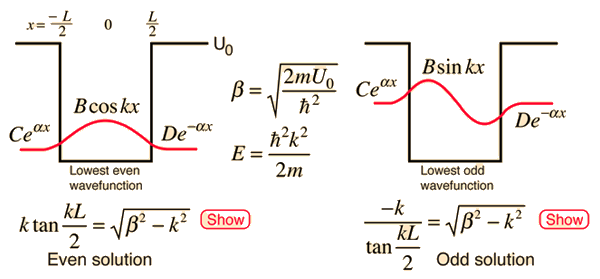
Hello forum, I have a question regarding the delta function potential well. Given the following potential: V(x) = -αδ(x) for -a/2 0.

3.) Since any excited state has energy larger than the first excited state, it follows that all excited states have E>0. 4.) But, every 1D potential has at least one bound state. So, it must be the ground state.

Does this sound like a reasonable argument? I don't think it quite works. For instance, point 2 is a non sequitur. You implicitly assume a bound mode exists and describe the shape of the corresponding bound wave function. However, then you proceed to argue that the mode must be unbounded, which would mean it's shape is not as you describe. Also, point 4 is not correct. Not all 1-D potentials have bound states.

Consider the delta 'spike,' [itex]V(x)= alpha delta (x)[/itex], as an example. I think the best conceptual argument is as follows: Consider a finite square well. You will notice, that as you make the well narrower and narrower, there start to be less and less bound mode solutions, until you are left with only one, even parity, bound solution. However, no matter how narrow you make the well(in other words, how close you get to the delta well limit), this one last bound mode will not go away.

Hello G01, 'Also, point 4 is not correct. Not all 1-D potentials have bound states. Gran Turismo 5 Pc Utorrent Softonic on this page. Consider the delta 'spike,' V(x)=αδ(x), as an example.' This is correct of course. But, point 4 is still valid for the given potential.

To keep a similar degree of generality it could be rephrased as: all atractive 1d potentials have at least one bound state. 'However, then you proceed to argue that the mode must be unbounded, which would mean it's shape is not as you describe.'

I disagree on this one. In this step I merely state that an excited state cannot be bound for this potential. The node theorem is a general result ( i'm quite sure about this) and has nothing to do with the potential shape. 'However, no matter how narrow you make the well(in other words, how close you get to the delta well limit), this one last bound mode will not go away. ' I don't exactly see that this line of reasoning proves the point. With this statement you also implictly assume that a bound mode exists. 'However, then you proceed to argue that the mode must be unbounded, which would mean it's shape is not as you describe.'